Eksponentielle funktioner
En eksponentiel funktion beskriver en eksponentielle udvikling.

Edited: 2018-01-21 05:09
Eksponentielle funktioner har funktionsforskriften f(x)=b*a^x
Man bruger de eksponentielle funktioner til, at beskrive en eksponentiel udvikling, som enten kan være aftagende, eller stigende. Udviklingen kan også vises grafisk, som vist på billedet til venstre.
Funktionen er stigende når a er større end 1, og aftagende når a ligger imellem 0 og 1, et eksempel kan ses nedenfor:
Formlen for kapitalfremskrivning
Formlen for kapitalfremskrivning er det samme som funktionsforskriften, der er dog enkelte forskelle. Den første er navngivningen på variablerne, hvor man bruger Kn i stedet for f(x), K0 i stedet for b og n i stedet for x. Bemærk også at a bliver erstattet af (r+1), som er fremskrivningsfaktoren.
Kn=K0*(1+r)^n
Grafer for eksponentielle funktioner
De eksponentielle funktioner danner normalt enten aftagende eller voksende grafer, et eksempel på en graf som er voksende, kan ses nedenfor:
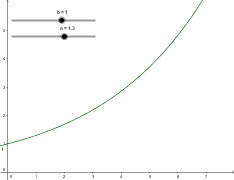
I dette eksempel havde vi en vækst på 30%, dvs a=1,3, med en begyndelsesværdi på 1 i X0.
Grafen for en aftagende funktion vil derimod se sådan ud:
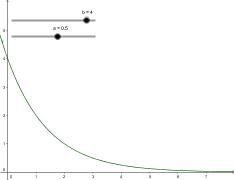
Det ses måske ikke så tydeligt, men grafen har en startværdi i X0 på 4 og en fremskrivningsfaktor som er a=0.5, hvilket svare til 50%. Det resultere i, at hver gang man går en hen på x-aksen, vil y altså aftage med 50%.

Fortæl os hvad du tænker: