Harmonikamodellen i matematik
En forklaring på harmonikamodellen med medfølgende formler og eksempler.

Edited: 2017-06-13 07:00
Harmonikamodellen er blot endnu en dårlig dansk ”fag” beskrivelse, som ikke har meget med matematik at gøre i sig selv. Betegnelsen "harmonikamodel" kan være forvirrende og vildledende, men det er egentlig meget enkelt, når man tænker på hvordan en harmonika fungere.
Når der tales om ”Harmonika-modellen” er der tale om procent og rente regning, og forskellige formler til regning imellem årlig rente og månedlig rente, osv.
Når man eksempelvis omregner en årlig rente til en månedlig rente, kan man sige at ”harmonikaen” bliver presset sammen, det modsatte vil ske hvis vi omregner omvendt – deraf betegnelsen "Harmonikamodel". Det kan være meget forvirrende for mange, men det vil nok alligevel give mening, når man begynder at se på formlerne. Men det giver sig selv, at en måned er kortere end et år, og at den renten om måneden vil værre mindre..
Det er imidlertid ikke nok kun at dividere, da vi jo også må tage højde for rentes rente. Mere om det i de følgende afsnit!
Fra årlig rente til månedlig rente
Hvis vi har en fast årlig rente på 10%, og ønsker at finde den månedlige rente, må vi først finde fremskrivningsfaktoren for vores årlige rente, da vi senere skal bruge den til at regne os frem til den månedlige rente.
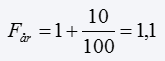
Den månedlige fremskrivnings faktor er den 12 rod af den årlige, som vist nedenfor:
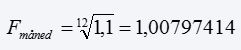
Vi runder resultatet op til 1,008, og går videre nu videre til at udregne renten i procent per år. For at gøre det, skal vi blot trække 1 fra og gange med 100. Mange vil med rutine, kunne se at, at ovenstående resultat giver en månedlig rente på 0,8 procent, uden at skulle foretage det sidste skridt – men til dem som er interesseret, så kan man regne det ud på følgende måde:
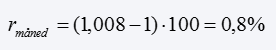
Fra månedlig rente til årlig rente
I dette eksempel ved vi, at den årlige rente skal være 10%, så for nu at regne os tilbage til den årlige rente fra en rente på 0,8%, må vi igen finde fremskrivningsfaktoren først:
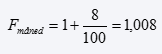
Derefter kan vi indsætte fremskrivningsfaktoren i vores formel, og det vil give os følgende:
Gennemsnitlig procentvis ændring
Hvis renten ikke er den samme år fra år, bliver det lidt mere kompliceret, og vi bliver nød til først at finde fremskrivningsfaktoren for alle årene enkeltvis. Hvis vi har følgende stigninger for over 4 år:
- Første år: 05%
- Andet år: 15%
- Tredje år: 19%
- Fjerde år: 14%
Vil det give os følgende fremskrivningsfaktorer:
- Første år: 1,05%
- Andet år: 1,15%
- Tredje år: 1,19%
- Fjerde år: 1,14%
For nu at finde fremskrivningsfaktoren for alle 4 år, ganger vi dem med hinanden:
Og til sidst kan vi så finde fremskrivningsfaktoren for 1 år via harmonikamoddelen:
Endeligt, for at finde den gennemsnitlige procentvise ændring, mangler vi kun at trække 1 fra og gange med 100. Men det behøver vi ikke, da vi bare kan omskrive fremskrivningsfaktoren direkte, så de 1,13 bliver til 13%. Men ellers kan man hurtigt regne det ud, eks.:
Procentændring=(1,131318-1)*100=13%

Fortæl os hvad du tænker: